摘自维基百科:蒙提霍尔问题,亦称为蒙特霍问题或三门问题(英文:Monty Hall problem),是一个源自博弈论的数学游戏问题,大致出自美国的电视游戏节目Let's Make a Deal。问题的名字来自该节目的主持人蒙提·霍尔(Monty Hall)。这个游戏的玩法是:参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车或者是奖品,选中后面有车的那扇门就可以赢得该汽车或奖品,而另外两扇门后面则各藏有一只山羊或者是后面没有任何东西。当参赛者选定了一扇门,但未去开启它的时候,知道门后情形的节目主持人会开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门会否增加参赛者赢得汽车的机会率?如果严格按照上述的条件的话,答案是会。—换门的话,赢得汽车的概率是2/3。
这着实是一个令人费解答案,尽管这是一个事实。一个比较常见的解释是通过枚举说明情况。如果门口的物品分别为汽车、羊A和羊B,参赛者选择转换答案,则存在以下三个等概率事件:
- 参赛者挑汽车,主持人挑两头羊的任何一头,转换将失败;
- 参赛者挑A羊,主持人挑B羊,转换将赢得汽车;
- 参赛者挑B羊,主持人挑A羊,转换将赢得汽车;
这是一个让人无法反驳的陈述,对此,只能是无话可说。但是你很可能还是想不通为何不是1/2。尽管你知道2/3是正确答案,但是却不明白1/2的问题出在哪里了。当主持人去除一个错误答案后,只剩下两个选择,1/2真是一个让人难以拒绝的答案,不是吗?接下来,我们计算一组概率。
为了方便分别用\(A\),\(B\),\(C\)代表山羊A(Goat A)、山羊B(Goat B)和汽车(Car);把三个门编号为1,2,3,并用\(A=1\)这样的表达方式代表山羊A在1号门这个事件,以此类推;而选择1号门的概率简记为\(P(1)\);记\(Y\)和\(N\)分别为转换选择和坚持原选择;将获得汽车记为事件\(W\),将获得山羊记为事件\(L\)。首先,考虑参赛者是否转换答案为等概随机事件的情况,计算获胜的平均概率
$$
\begin{split}
P(W) &=~~~~P(C=1)[P(1)P(N)+P(2)P(Y)+P(3)P(Y)] \\
& ~~~~+P(C=2)[P(2)P(N)+P(1)P(Y)+P(3)P(Y)] \\
& ~~~~+P(C=3)[P(3)P(N)+P(1)P(Y)+P(2)P(Y)]
\end{split}
$$
上面的表达式包含了所有的情况(当然,这里有偷工减料,忽略了主持人的行为。实际上,当参赛者第一次选错时,主持人的行为已经确定,概率为1;而当参赛者第一次选对时,只有主持人从错误选择中随机选择一个剔除;两种情况的概率和为1)。上述公式的意思是把获得汽车这个事件拆成三个事件的组合,即“在门后安放车和羊+参赛者选择一个门+参赛者确认门”。不难计算\(P(W)=1/2\)。也就是说,如果这时候参赛者瞎猜一个答案,那么他获得汽车的概率是1/2。所以1/2也是没有错的,但这是建立在随机选择的基础之上。
接下来,变换策略。假设参赛者非常相信自己的直觉,一旦选定答案之后,就不再做出更改,这时候计算他能赢得汽车的概率
$$
P(W) =P(C=1)P(1)P(N)+P(C=2)P(2)P(N)+P(C=3)P(3)P(N) \\
$$
这时,\(P(N)=1\)也很容易计算出\(P(W)=1/3\)。很可惜,这时候专一并没有带来好运。
若在每次主持人询问是否确定答案时,参赛者都改变其选择,那么他能赢得汽车的概率为
$$
\begin{split}
P(W) &=~~~~P(C=1)[P(2)P(Y)+P(3)P(Y)] \\
& ~~~~+P(C=2)[P(1)P(Y)+P(3)P(Y)] \\
& ~~~~+P(C=3)[P(1)P(Y)+P(2)P(Y)]
\end{split}
$$
很容易计算出来,这时获胜的概率是2/3。所以,不能怪参赛者喜新厌旧,就是因为人不断追寻新的东西才社会才不断进步和发展的[奸笑],至少,能赢得汽车不是?
最后,再献上一个简略的C++仿真程序,
// MontyHallProblem.h
#pragma once
#include <cstdlib>
class MontyHallProblem
{
public:
MontyHallProblem();
~MontyHallProblem();
void initialize();
void choose(unsigned choice);
bool verify(bool change);
private:
unsigned prize;
unsigned choice;
};
//MontyHallProblem.cpp
#include "MontyHallProblem.h"
MontyHallProblem::MontyHallProblem()
{
}
MontyHallProblem::~MontyHallProblem()
{
}
void MontyHallProblem::initialize()
{
prize = rand() % 3;
}
void MontyHallProblem::choose(unsigned choice)
{
this->choice = choice;
}
bool MontyHallProblem::verify(bool change)
{
if (choice == prize)
{
return !change;
}
else
{
return change;
}
}
// main.cpp
#include <iostream>
#include "MontyHallProblem.h"
using namespace std;
int main()
{
MontyHallProblem p;
unsigned total = 10000;
cout << "-------------------------------------------------\n";
cout << "| Probability \t| car\t\t| goat \t\t|\n";
cout << "-------------------------------------------------\n";
// 随机选择
float success = 0, failure = 0;
for (size_t i = 0; i < total; i++)
{
p.initialize();
int choice = rand() % 3;
p.choose(choice);
bool change = rand() % 2;
if (p.verify(change))
{
success++;
}
else
{
failure++;
}
}
cout << "| Random choice\t| " << success / total << "\t| "<< failure/total << "\t|" << endl;
cout << "-------------------------------------------------\n";
// 始终转换答案
success = 0; failure = 0;
for (size_t i = 0; i < total; i++)
{
p.initialize();
int choice = rand() % 3;
p.choose(choice);
bool change = true;
if (p.verify(change))
{
success++;
}
else
{
failure++;
}
}
cout << "| Keep changing\t| " << success / total << "\t| " << failure / total << "\t|" << endl;
cout << "-------------------------------------------------\n";
// 始终坚持原选择
success = 0; failure = 0;
for (size_t i = 0; i < total; i++)
{
p.initialize();
int choice = rand() % 3;
p.choose(choice);
bool change = false;
if (p.verify(change))
{
success++;
}
else
{
failure++;
}
}
cout << "| Never change \t| " << success / total << " \t| " << failure / total << " \t|" << endl;
cout << "-------------------------------------------------\n";
return 0;
}
未经允许不得转载:Charlie小站 » 三门问题(Monty Hall problem)
 Charlie小站
Charlie小站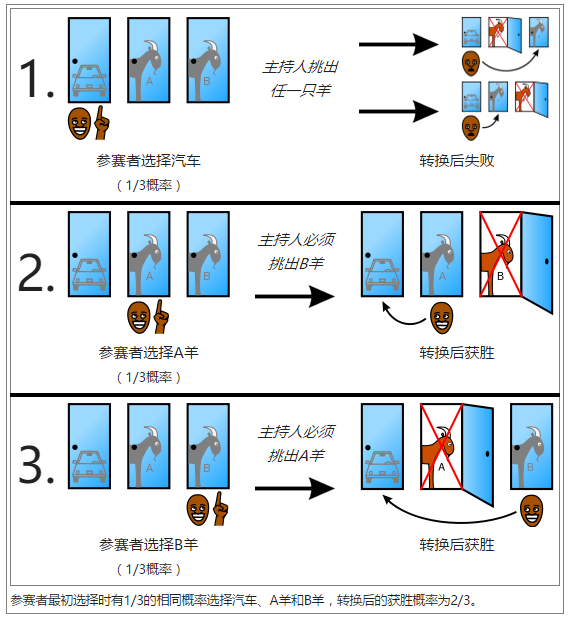

 单位速度参数化
单位速度参数化 procrustes分析原理与应用
procrustes分析原理与应用 用C语言画颗心(三)——着色
用C语言画颗心(三)——着色 用C语言画颗心(二)——光照模型
用C语言画颗心(二)——光照模型 用C语言画颗心(一)——心形曲面
用C语言画颗心(一)——心形曲面
评论前必须登录!
登陆 注册