【题】设实数\(a\),\(b\),\(c\),\(d\)满足\(a\ge b\ge c\ge d \gt 0\),且\(a+b+c+d = 1\).证明:
\begin{equation}
(a+2b+3c+4d)a^ab^bc^cd^d \lt 1
\end{equation}
【证】我们知道,函数\(f(x)= p^t, (0\lt p \lt 1)\)在其定义域上为减函数。所以根据题设可知
\begin{equation}
a^a \le a^d,b^b \le b^d,c^c\le c^d
\end{equation}
所以\(a^ab^bc^cd^d \le a^db^dc^dd^d = (abcd)^d\)。又由均值不等式知
\begin{equation}
abcd \le \left(\frac{a+b+c+d}{4}\right)^4
\end{equation}
结合以上,有
\begin{align}
\text{左边} &=(a+2b+3c+4d)a^ab^bc^cd^d \\
&\le (a+2b+3c+4d)(abcd)^d \\
& \le (a+2b+3c+4d)\left(\frac{a+b+c+d}{4}\right)^{4d} \\
& \lt (4a+4b+4c+4d)\cdot\frac{1}{4} \\
&= 4\cdot \frac{1}{4} \\
&= 1
\end{align}
未经允许不得转载:Charlie小站 » IMO2020第二题解答
 Charlie小站
Charlie小站
 用C语言画颗心(一)——心形曲面
用C语言画颗心(一)——心形曲面 单位速度参数化
单位速度参数化 procrustes分析原理与应用
procrustes分析原理与应用 用C语言画颗心(三)——着色
用C语言画颗心(三)——着色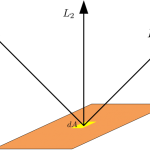 用C语言画颗心(二)——光照模型
用C语言画颗心(二)——光照模型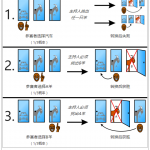 三门问题(Monty Hall problem)
三门问题(Monty Hall problem)
评论前必须登录!
登陆 注册