在上一篇文章用C语言画颗心(一)——心形曲面中,我们已经能用字符拼出一个心形图案。这一次,我们通过模拟光照模型,让心形表现出立体感。
说到光照(辐射)模型,博主学过一点点,什么照度,亮度,立体角,反射率,概念挺多,我也记不全。知乎原贴用的兰伯特体(Lambertian)假设,那我也用用吧。
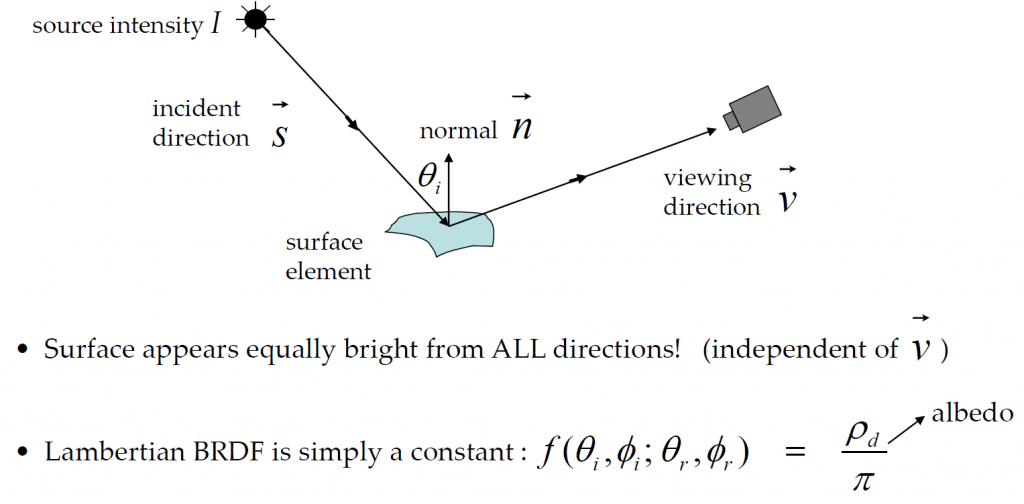
Lambertian表面最主要的性质为在各个方向上的辐射相等,如上图所示,\(L_1 = L_2 = L_3\);并且,Lambertian表面完全反射,这就使得物体表面的双向表面函数是一个常数,如下图所示
更重要的一个结论是,表面亮度与入射方向和物体表面法向量的夹角余弦成正比,即$$L(x,y,z) \propto \alpha = \cos(\vec{n}(x,y,z),\vec{s})$$在应用时,我们直接令\(L = \max(\alpha,0)\)。
如何将亮度映射到字符上呢,偷懒抄的知乎原贴,用".:-=+#%@"用这些字符区分亮度等级,亮度从小到大。一切准备就绪,可以准备敲代码了。
一,算梯度。梯度的算法在上一篇中已经提到,这里回忆一下$$\nabla f(x,y,z) = \left[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right]$$上一次我们只确定了\(x\)和\(z\)的取值范围,我们通过二分法去解\(y\):
double compute_y(double x, double z){
double z_min = 0.0, z_max = 1.5;
double eps = 1e-6, r = 1.0, y;
while(r>eps){
y = (z_min + z_max) / 2.0;
if (f(x,y,z) == 0)
return y;
if (f(x,y,z) > 0)
z_max = y;
else
z_min = y;
r = z_max - z_min;
}
return 0.5*(z_max + z_min);
}
二,画图。需要注意的一点,由于图像坐标系和数学坐标系的\(z\)轴方向相反,需要按照递减的方式循环,
int main(int argc, char const *argv[])
{
double y, nx, ny, nz, a;
// 光源方向(入射光方向)
double lx = 1, ly = 1, lz = -1;
char *l = ".:-=+#%@";
for (float z = 1.5; z > -1.5; z-=0.1)
{
for (float x = -1.5; x < 1.5; x+=0.05)
{
// 点在心形图内
if (f(x,0,z) < 0)
{
// 计算y
y = compute_y(x,z);
// 计算梯度(法向量)
nx = fx(x,y,z);
ny = fy(x,y,z);
nz = fz(x,y,z);
// light source direction (1,1,-0.5)
a = (lx*nx + ly*ny + lz*nz)/sqrtf(lx*lx+ly*ly+lz*lz)
/sqrtf(nx*nx+ny*ny+nz*nz);
// 显然,正面的夹角余弦为正值
// 根据入射光与法线夹角余弦值计算光强
putchar(l[(int) ((0.5 * a + 0.5)*6)]);
}
else
putchar(' ');
}
putchar('\n');
}
return 0;
}
完整的程序戳这里。效果图如下
未经允许不得转载:Charlie小站 » 用C语言画颗心(二)——光照模型
 Charlie小站
Charlie小站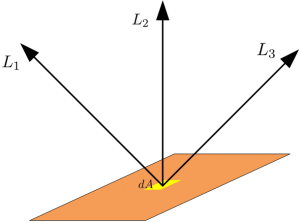


 单位速度参数化
单位速度参数化 procrustes分析原理与应用
procrustes分析原理与应用 用C语言画颗心(三)——着色
用C语言画颗心(三)——着色 用C语言画颗心(一)——心形曲面
用C语言画颗心(一)——心形曲面
评论前必须登录!
登陆 注册